This article will discuss open quantum systems and the master equations. We’ll start by defining open quantum systems and then derive the master equations.
An open quantum system is described as a system that interacts with an environment, which is also a quantum system. Such situations are realized when such situations include spontaneous emission from a two-level atom and Rabi oscillation, where an atom interacts with an electromagnetic field.
In many cases, it is straightforward to calculate the unitary operator governing the evolution of an open quantum system in interaction with a finite and small environment. For example, a two-level quantum system interacts with a two-level environment. However, when an infinite dimensional quantum system, such as a harmonic oscillator, interacts with a large and infinite dimensional environment, it may be difficult to find out the exact dynamics of the system alone. In these cases, we resort to master equations, which provide the system’s dynamics under certain approximations.
Consider a total system-environment Hamiltonian as
\begin{equation}
\hat{H} = \hat{H_S} + \hat{H_E} + \hat{H}_{SE} \nonumber
\end{equation}
where \(\hat{H_S}\), \(\hat{H_E}\), and \(\hat{H_{SE}}\) denote the system, environment, and system-environment interaction Hamiltonians
Let us denote the full initial state of the system and the environment by \(\rho(0)\) and \(U(t)\) to be the unitary time evolution operator for our full system. Then, we can write the state of the system and environment at time \(t>0\) as
\begin{equation}
\rho(t) = U(t) \rho(0) U^{\dagger}(t) \nonumber
\end{equation}
We can find out the dynamics of the system alone as it interacts with the environment by taking a partial trace of the full state of the environment
\begin{equation}
\rho_{S}(t) = Tr_E[U(t) \rho(0) U^{\dagger}(t)]
\end{equation}
We assume that the initial density operator factorizes into that for the system and that for the environment. When we deal with an infinitely large environment, we can safely assume that since the state of the environment remains unaffected by the system:
\begin{equation}
\rho(t) \approx \rho_S(t) \otimes \rho_E(0) \nonumber
\end{equation}
We further assume that the state of the environment may be chosen to be represented by a thermal state at a fixed temperature, \(T\) as
\begin{equation}
\rho_E = \frac{e^{-\beta_T \hat{H_E}}}{Tr(e^{-\beta_T \hat{H_E}})}, \hspace{15pt} \beta_T= \frac{1}{K_B T} \nonumber
\end{equation}
With these assumptions, one proceeds to derive an evolution equation for the system alone – the master equation- by resorting to further approximation referred to as the Born Markov approximation by retaining terms to second order in the system-bath interaction Hamiltonian followed by the assumption that the correlation time of the bath is much shorter than the time scale over which the system evolves.
If we denote the system-environment Hamiltonian by
\begin{equation}
\hat{H}_{SE} = \sum_{\alpha}S_{\alpha} E_{\alpha}\nonumber
\end{equation}
Then, the master equation under Born and Markov approximations can be expressed as
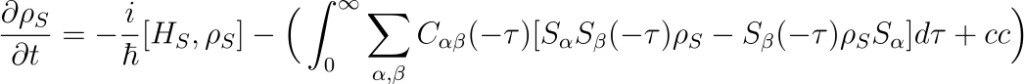
Where the bath correlation functions are defined as
\begin{equation}
C_{\alpha \beta}(-\tau) =\frac{1}{\hbar^2} \langle E_{\alpha} E_{\beta}(-\tau) \rangle \nonumber
\end{equation}
\begin{equation}
C_{\alpha \beta}(-\tau) = \frac{1}{\hbar^2} Tr[ \rho_B E_{\alpha} E_{\beta}(-\tau) ] \nonumber
\end{equation}
and the operators with time dependence can be calculated as
\begin{equation}
S_{\beta}(-\tau) =e^{-\frac{iH_S \tau}{\hbar}} S_{\beta} e^{\frac{iH_S \tau}{\hbar}} \nonumber
\end{equation}
\begin{equation}
E_{\beta}(-\tau) =e^{-\frac{iH_E \tau}{\hbar}} E_{\beta} e^{\frac{iH_E \tau}{\hbar}} \nonumber
\end{equation}
The above-given master equation describes the dynamics of an open quantum system interacting with its environment derived under-born- Markov approximation. This master equation is independent of the structure of the system and the environment Hamiltonian, so we can use it to derive the master equation for our physical model.
Our physical model consists of a harmonic oscillator at frequency \(\omega_0\), which interacts with a heat bath at temperature \(T\). The relevant Hamiltonians for this model are given as
\begin{equation}
H_S = \hbar \omega_0 a^{\dagger}a, \hspace{5pt} H_B = \sum_j \hbar \omega_j a_j^{\dagger}a_j
\end{equation}
\begin{equation}
H_{SB} = \hbar \sum_j i g_j (a + a^{\dagger}) (a_j – a_j^{\dagger})
\end{equation}
Where \(H_S\), \(H_B\), and \(H_{SB}\) denote the system, bath, and system-bath interaction Hamiltonians.
To derive the master equation for our physical model, we can use the structure of the master equation given above. The final master equation for the harmonic oscillator, coupled to heat bath under Born- Markov approximation, can be found to be
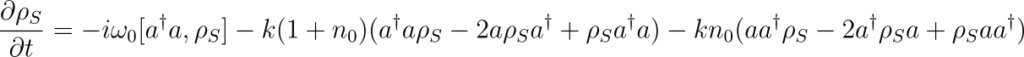
Where \(
k = \pi \sum_j g_j^2 \delta(\omega_j – \omega_0), \hspace{10pt} n_0 = \frac{1}{e^{\beta \hbar \omega_0} – 1} \) are dependent on the properties of the bath.
If we take the initial state of our system represented by density operator \(\rho_S(0)\), then under the given master equation, the state of the system at any time \(t\) will be \(\rho_S(t)\) and after a long time, the system will be in equilibrium with the environment and its state will be a thermal state characterized by the frequency \(\omega_0\) and temperature \(T\). This can be represented mathematically as
\begin{equation}
\rho_S(0) \xrightarrow{ME} \rho_S(t) \nonumber
\end{equation}
\begin{equation}
\rho_S(t) \xrightarrow{ME} (1-e^{-\beta \hbar \omega_0}) e^{-\beta\hbar \omega_0 a^{\dagger}a} \nonumber
\end{equation}
Where \(\beta= \frac{1}{K_B T}\) and \(e^{-\beta \hbar \omega_0} = \frac{n_0}{1+n_0}\)
The given master equation for a harmonic oscillator is known to have a property that it evolves Gaussian states into themselves. This will be discussed further in upcoming sections after solving the master equation using thermo-field dynamics notation and an operator method.
References:
[1] Agarwal, G. (2012). Quantum optics. Cambridge University Press.
You might be interested in other articles on:


