Quantum Thermodynamics 2024 Unique Frameworks of 1st and 2nd Law

This article provides an explanation of the first and second laws of quantum thermodynamics. These laws provide different definitions of heat and work and introduce new forms of energy. In classical thermodynamics, the first law states that the change in internal energy of the system is equal to the sum of the amount of heat exchanged and the work done. However, when we deal with thermodynamics in the quantum regime, the first law might differ from the classical case. Quantum thermodynamics is a rapidly evolving field due to its importance in quantum technology. It involves studying the thermodynamic properties of a quantum system. We will cover thermodynamics in the quantum regime, its fundamental aspects, and new directions.

An Overview of Classical Thermodynamics

Classical thermodynamics strives to provide a description of systems at the macroscopic level. Its significant contributions to industrial revolutions stem from its successful applications in heat engines, refrigerators, and understanding the role of entropy in chemical reactions. Using macroscopic variables such as pressure, temperature, and volume, thermodynamics defines the state of a system. Its ultimate aim is to study the heat and work and their relation with the entropy of a system. These forms of energy are crucial as they offer valuable insights into the efficiency and power of a machine and how to optimize it for improved efficiency.

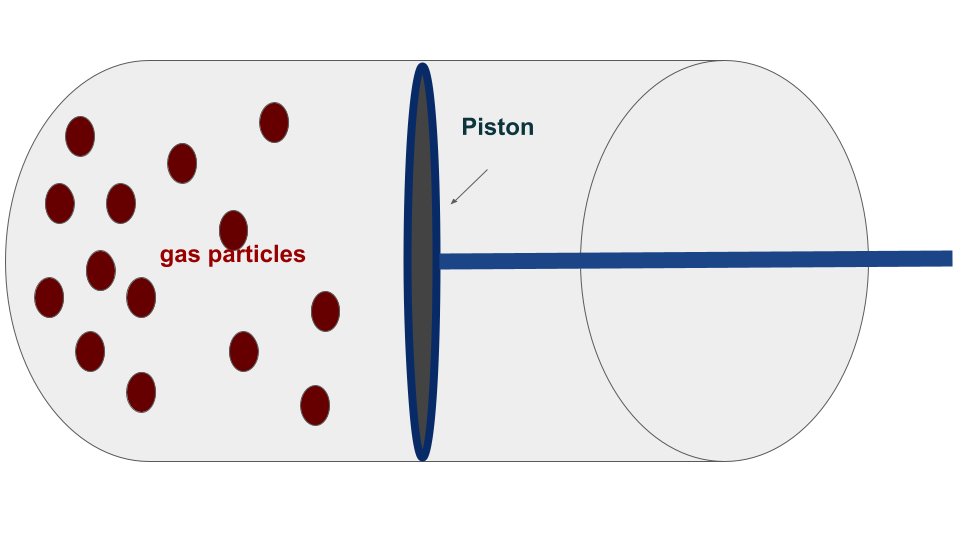
In classical thermodynamics, we can start by discussing the forms of the first and second laws. To understand the equations involved, let’s consider a standard macroscopic system consisting of a gas cylinder with a piston that is free to move. When we heat the gas, it expands and pushes the piston up, resulting in the gas performing work on the piston. Similarly, if an external pressure is applied to the piston such that it exceeds the internal pressure of the gas, the volume of the gas inside the piston decreases, and work is performed on the gas.

If the cylinder walls allow for heat transfer, heat exchange may occur between the gas and the environment. The expression of this work and heat depends on whether the given process is reversible or irreversible.

Second Law of Classical Thermodynamics

The second law of classical thermodynamics states that the total entropy production during a process is always non-negative. Consider a general macroscopic system (S) interacting with some environment (E). When this system interacts with the environment, there will be some entropy production in the full system+environment model. This entropy production ( \Sigma \) is always non-negative.

$$ \Sigma \geq 0 $$

During the interaction of the system with the environment, the heat flown from \(S\) to \(E\) is \(Q\) at a temperature of \(T\), then the entropy production is the sum of the change in entropy of the system and the entropy that flown from system to environment at a given temperature.

$$ \Sigma = \Delta S_S + \frac{Q}{T} \geq 0 $$

A process is reversible if the entropy production is zero; otherwise, it is irreversible.

First Law of Classical Thermodynamics

The definition of heat and work in the classical case is different for reversible and irreversible processes. To proceed further, we can go back to our example of a gas confined in a cylinder along with a piston that is free to move. Let’s Split the definitions into two different parts:

Reversible Processes

A reversible process is always taken as a quasistatic process. The transformation in such processes is taken out to be infinitely slow so that the system remains at equilibrium with the environment at each point in time. Since in quasistatic processes, the system (gas particles) is always in equilibrium with the environment (external pressure on the piston), the pressure of the gas is the same as that of external pressure. During such a process, taking \(dV\) to be the change in volume of the gas, then the work done by the gas is given by:

$$ W = – \int P_{gas} dV $$

If \( \Delta U \) is the change in internal energy of the system (gas), then the first law states that:

$$ \Delta U = W + Q $$

The term \(Q\) is the amount of heat flown into the system.

Irreversible Processes

An irreversible process is not quasistatic but an instantaneous process. The transformation is taken out very rapidly such that the system will not have enough time to come to equilibrium. . During such a process, taking \(dV\) to be the change in volume of the gas, then the work done by the gas is given by:

$$ W = – \int P_{ext} dV $$

Where \( P_{ext} \) is the external pressure on the piston.

First Law of Quantum Thermodynamics (Using Standard Definitions)

The classical form of the first law of thermodynamics is splitting the change in internal energy in heat and work. This section aims to show that we can find equivalent expressions for heat and work. To do so, we use the standard definitions of heat and work. These definitions are

Work: The work realized on or by the working substance is the change in the internal energy accompanied by a change in the generalized coordinates.

Heat: The heat exchanged between the working substance and the external environment corresponds to the change in the internal energy that is accompanied by entropy change.

Consider that our quantum system Hamiltonian is \( \hat{H_S} = \sum_{n} E_n |n \rangle \langle n| \), where \( |n \rangle \) and \( E_n \) are the eigenstates and eigenenergies of the system. The internal energy \( U \) of the system can be defined as
\begin{equation}
U = \langle\hat{H_S}\rangle = tr({\hat{\rho} \hat{H_S}}) = \sum_{n} P_n E_n \nonumber
\end{equation}
Where \( P_n = \langle n| \hat{\rho}|n \rangle \) and \(\hat{\rho}\) denotes the density operator of the system. So, the change in the internal energy of the system can be written as
\begin{equation}
dU = \sum_n [E_n dP_n + P_n dE_n] \nonumber
\end{equation}
The change in internal energy of the system can be expressed as the sum of work done and heat exchanged between the system and the environment. Work is defined as the changes in generalized coordinates. In quantum mechanics, changes in generalized coordinates lead to changes in energy-level configuration. Thus, the terms corresponding to \(dE_n \neq 0\) will contribute to the expression of work. By using this methodology, the first law of quantum thermodynamics can be expressed as
\begin{equation}
dU = dW + dQ \nonumber
\end{equation}
Where \(dQ = \sum_n E_n dP_n \) and \( dW = \sum_n P_n dE_n \).

Quantum Thermodynamics Framework Using Wigner Phase-Space Description

In this section, we present a framework of quantum thermodynamics specifically provided by the dynamics of a quantum Brownian oscillator.

The master equation for a quantum Brownian oscillator of frequency \(\omega\) in contact with a heat bath at temperature T:

$$ \frac{\partial}{\partial t} \rho = -\frac{i}{\hbar} [\frac{\hat{p}^2}{2m} + \frac{1}{2} m \omega^2 \hat{q}^2, \rho] – \frac{2 \kappa m \omega}{\hbar} [n(\omega,T) + \frac{1}{2}]([\hat{q},[\hat{q},\hat{p}]]) – \frac{i \kappa}{\hbar} ([\hat{q},\{\hat{}p,\rho \}])$$

\( \hat{q}: \text{Position Operator} \)

\( \hat{p}: \text{Momentum Operator} \)

Using the winner phase space description, the above master equation is converted into a Fokker-Planck equation for \(\hat{\rho} \rightarrow W(q,p) \).

$$ \frac{\partial}{\partial t} W(q,p,t) = \Big \{ -\frac{\partial}{\partial q}(\frac{p}{m}) + \frac{\partial}{\partial p}[2 \kappa p + (\frac{\partial V(q,a)}{\partial q})] + D\frac{\partial^2}{\partial p^2} \Big \} W(q,p,t) $$

$$ V(q,a) = \frac{1}{2}aq^2, \hspace{1pt} a = m\omega^2 $$

$$ D = 2 m\hbar \omega \kappa [n(\omega,T)+1/2],\hspace{1pt} n(\omega,T) = \frac{e^{-\beta \hbar \omega}}{1 – e^{-\beta \hbar \omega}} $$

The associated Langevin equations for the above Fokker-Planck equation are as follows:

$$ \dot{q} = \frac{p}{m} $$

$$ \dot{p} = -2 \kappa p – \frac{\partial }{\partial q} V(q,a) + f(t) $$

$$ \langle f(t) f(t’) \rangle = 2 D \delta(t-t’) $$

These Langevin equations are combined to derive the expressions of heat work and change in internal energy. We will present the final expressions below:

$$ Q = [-2\kappa p + f(t)] dq $$

$$ W = -\frac{\partial V(q,a)}{\partial a} da $$

$$ dU = d(p^2/2m + V) $$

To calculate the heat, work, and change in internal energy, one must calculate the stochastic averages of the above thermodynamic quantities.

First & Second Law of Quantum Thermodynamics (For Autonomous Quantum Systems)

In this section, we provide a framework of quantum thermodynamics specifically tailored for autonomous quantum systems.

A quantum system \(S\) is interacting with another quantum system \(B\) such that the quantum system \(B\) is acting as an energy source of heat and work for \(S\). This can be pictured as shown in the below image.

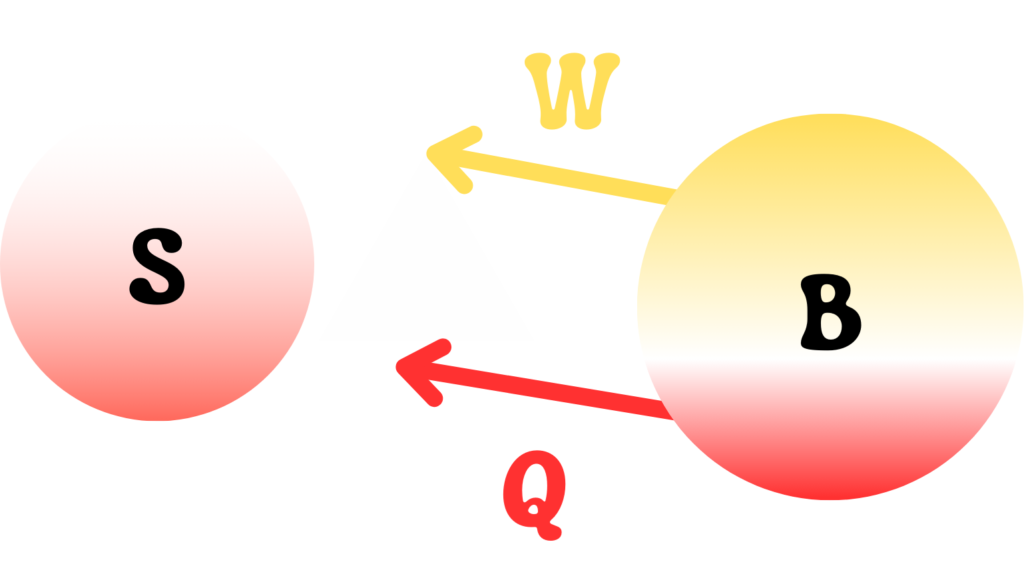
The reduced states of both systems at any time \(t\) are \(\rho_S\) and \(\rho_B\) respectively. During the interaction, the heat provided by \(B\) to \(S\) is negative of the variation of thermal energy of \(B\).

$$ Q = – \Delta E_B^{th} = – \Delta Tr[ \hat{W} \hat{H_B} ]$$

The term \( E_B^{th} \) denotes the thermal energy of B in the state \( \rho_B \) and \(\hat{H}_B\) is the hamiltonian of \(B\). \( \hat{W} \) is an equilibrium state with the same von Neumann entropy as of \( \rho_B \). If \( S_{VN} \) denotes the von-Neumann entropy then

$$ S_{VN}[\rho_B] = S_{VN}[\hat{W}] $$

This heat exchange causes a change in the internal energy. If \( \Delta E^{tot} \) represents the change in internal energy of B, then the remaining energy can be attributed to the work done \(W\) by \(B\).

$$ W = -\Delta E^{tot} – Q $$

The internal energy is the expectation value of the Hamiltonian with respect to the density operator for that system.

The above-given expressions for heat and work are also consistent with the second law of thermodynamics. During the transformation of \(S\) the entropy production for \(S\) is

$$ \sigma_S = \Delta S_{VN}(\rho_S) – \beta_B(0) Q \geq 0$$

The first term in the expression of \( \sigma_S \) is the change in the von Neumann entropy of system \(S\) and the term with initial inverse temperature \(\beta_B(0)\) of \(B\) is the entropy flown into S from B.

First Law of Quantum Thermodynamics (Using Coherent Energy)

This section is mainly centered around the development of a framework for quantum thermodynamics with particular emphasis on the quantum analog of the first law of classical thermodynamics. This interesting approach proposed by Bernardo is based on deriving an identity involving instantaneous eigenstates of the density operator, instantaneous eigenstates of the system Hamiltonian followed by identification of terms appearing therein consistent with other known and well-established notions. This approach leads to a formulation of the first law of quantum thermodynamics, containing, besides changes in internal energy, the work done, and the heat, a new quantity- change in the ‘coherent energy.’

This article shows that if we split a system’s change in internal energy into heat and work, it becomes inconsistent mathematically. However, this form is valid in classical thermodynamics. This inconsistency is overcome by introducing a new quantity called coherent energy, which only exists in the quantum domain, but in classical thermodynamics, there is no notion of it. It arises because of the change in the overlap of the basis of the system’s Hamiltonian and the system’s state. The mathematical structure of this law takes the following form:

$$ dU = dW + dQ + dC $$

If you encounter classical definitions of heat and work in this section, then refer to the standard definitions of heat and work provided in previous sections.

\(\)
$$ \hat{H} = \hat{H}_S + \hat{H}_E + \hat{H}_{SE} $$

Where \( \hat{H}_S \), \( \hat{H}_E \), and \( \hat{H}_{SE} \) denote the system, environment, and system-environment interaction Hamiltonians.

Consider that our system Hamiltonian is \( \hat{H_S} = \sum_{n} E_n |n \rangle \langle n| \), where \( |n \rangle \) and \( E_n \) are the eigenstates and eigenenergies of the system. The internal energy \( U \) of the system can be defined as
\begin{equation}
U = \langle\hat{H_S}\rangle = tr({\hat{\rho} \hat{H_S}}) = \sum_{n} P_n E_n \nonumber
\end{equation}
Where \( P_n = \langle n| \hat{\rho}|n \rangle \) and \(\hat{\rho}\) denotes the density operator of the system. So, the change in the internal energy of the system can be written as
\begin{equation}
dU = \sum_n [E_n dP_n + P_n dE_n] \nonumber
\end{equation}
The change in internal energy of the system can be expressed as the sum of work done and heat exchanged between the system and the environment. Work is defined as the changes in generalized coordinates. In quantum mechanics, changes in generalized coordinates lead to changes in energy-level configuration. Thus, the terms corresponding to \(dE_n \neq 0\) will contribute to the expression of work. By using this methodology, the first law of quantum thermodynamics can be expressed as
\begin{equation}
dU = dW + dQ \nonumber
\end{equation}
Where \(dQ = \sum_n E_n dP_n \) and \( dW = \sum_n P_n dE_n \).

Now, we will calculate the change in internal energy of the system in the eigenbasis of the density operator of the system. Assume that the state of our system is \( \hat{\rho} = \sum_{k} \rho_k |k \rangle \langle k| \), where \( |k \rangle \) and \( \rho_k \) are the eigenstates and eigenenergies of the system. The internal energy \(U\) of the system can be defined as
\begin{equation}
U = \langle\hat{H_S}\rangle = tr({\hat{\rho} \hat{H_S}}) = \sum_{k} \rho_k \epsilon_k\nonumber
\end{equation}
Where \( \epsilon_k = \langle k|{\hat{H_S}}|k \rangle \) and \( \rho_k = \langle k|{\hat{\rho}}|k \rangle \). So, the change in internal energy of the system can be expressed as:
\begin{equation}
dU = \sum_k [\epsilon_k d\rho_k + \rho_k d\epsilon_k] \nonumber
\end{equation}
Now, we will calculate the von Neumann entropy of our system using the formula

$$S = -k_B tr(\hat{\rho}\log(\hat{\rho})) = -k_B \sum_k \rho_k \log(\rho_k) $$

So, we can express a change in entropy as
\begin{equation}
dS = -k_B \sum_k \log(\rho_k) d\rho_k \nonumber
\end{equation}
where we have exploited the fact that \( \sum_k \rho_k = 1\) so \( \sum_k d\rho_k = 0\). When \(d \rho_k \neq 0\), we can observe a change in entropy. With that in mind, we can use the classical definition of heat to determine the expressions for work and heat as
\begin{equation}
\bar{d}Q = \sum_k \epsilon_k d\rho_k \hspace{15pt} \bar{d}W = \sum_k \rho_k d\epsilon_k \nonumber
\end{equation}
So, the first law of quantum thermodynamics can be expressed as
\begin{equation}
dU = \bar{d}Q + \bar{d}W \nonumber
\end{equation}
Now, we will see that the two definitions of heat and work are not equivalent mathematically. To rectify this inconsistency, the author introduced a new quantity called coherent energy \(dC\). We can easily calculate the following expressions:

\begin{equation}
\begin{aligned}
dW &= \sum_n P_n dE_n \\
&= \sum_n \langle n| \sum_k \rho_k |k \rangle \langle k|n \rangle dE_n \\
&= \sum_n \sum_k \rho_k |c_{n,k}|^2 dE_n \nonumber
\end{aligned}
\end{equation}

\begin{equation}
\begin{aligned}
\bar{d}W &= \sum_k \rho_k d\epsilon_k \\
&= \sum_k \rho_k d[\langle k| (\sum_n E_n |n \rangle \langle n|) |k \rangle] \\
&= dW + dC \nonumber
\end{aligned}
\end{equation}

Where \( dC = \sum_n \sum_k \rho_k E_n d|c_{n,k}|^2\) and \(|c_{n,k}|^2 = |\langle n | k \rangle|^2 \). We can similarly deduce that \( \bar{d}Q = \sum_n \sum_k |c_{n,k}|^2 E_n d \rho_k \) and \(dQ = \bar{d}Q + dC\)
As we can see from the above analysis, the two mathematical forms of work and heat are not equivalent. Therefore, we cannot write \(dU = dW + \bar{d}Q\). This inconsistency in the first law of quantum thermodynamics can be removed by adding the coherent energy term \(dC\). The author thus proposes a new definition of the first law of quantum thermodynamics:
\begin{equation}
dU = dW + \bar{d}Q + dC \nonumber
\end{equation}
For finite time processes, these quantities can be expressed as:
\begin{equation}
\begin{split}
W(t) &= \sum_{n} \sum_{k} \int_{0}^{t} \rho_k |c_{n,k}|^2 \frac{dE_n}{dt’} dt’ \\
Q(t) &= \sum_{n} \sum_{k} \int_{0}^{t} E_n |c_{n,k}|^2 \frac{d \rho_k}{dt’} dt’ \\
C(t) &= \sum_{n} \sum_{k} \int_{0}^{t} E_n \rho_k \frac{d |c_{n,k}|^2}{dt’} dt’ \\
\Delta U(t) &= W(t) + Q(t) + C(t)
\end{split}
\end{equation}

We have explored various versions of quantum thermodynamics frameworks. Additional versions of this framework exist outside of what we have covered. We will continue to update this article by adding more frameworks over time. If you have any suggestions to improve the article or would like to add more frameworks, please let us know via the comment box.

Frequently Asked Questions

References:

Agarwal, G. S., & Chaturvedi, S. (2013). Quantum dynamical framework for Brownian heat engines. Physical Review E, 88(1), 012130

Elouard, C., & Lombard Latune, C. (2023). Extending the Laws of Thermodynamics for Arbitrary Autonomous Quantum Systems. PRX Quantum, 4(2), 020309.pen_spark

Bernardo, B. L. (2020). Unraveling the role of coherence in the first law of quantum thermodynamics. Physical Review E, 102(6), 062152. doi:10.1103/PhysRevE.102.06215

To grasp the essence of quantum thermodynamics, delve into the insights offered in the following article.

https://quantumthermodynamic.com/what-is-quantum-thermodynamics/