In this article, we are going to learn about the operator method to solve the master equation in quantum optics. After discussing the master equation and foundations of thermo-field dynamics in previous articles, which can be found here –
[1] https://quantumthermodynamic.com/open-quantum-systems-and-master-equations/
[2] https://quantumthermodynamic.com/introduction-to-thermo-field-dynamics/
We are now in a position to discuss how we can find an exact solution to the master equation in quantum optics using thermo-field dynamics – which is called the operator method to solve the master equation and, in general, can be used to solve most of the master equations. In this article, we will solve the born-markov master equation of a harmonic oscillator of frequency \(\omega_0\), coupled to a heat bath at temperature \(T\) using operator method. We will see how the given master equation can be converted into a Schrödinger-like equation using TFD, which makes it easily solvable for an arbitrary initial state of the system.
To learn how we can use the operator method to solve the master equation, we start our discussion by looking at the born-markov master equation of a harmonic oscillator described above and coupled to a bath, which is made up of many harmonic oscillators. This physical model is also discussed in the previous two articles.
For our physical model described above, the master equation under Born- Markov approximation for the system is given as
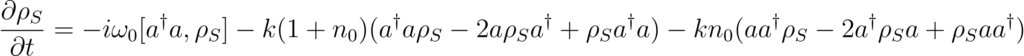
Where \(
k = \pi \sum_j g_j^2 \delta(\omega_j – \omega_0), \hspace{10pt} n_0 = \frac{1}{e^{\beta \hbar \omega_0} – 1} \) are dependent on bath.
Using equations from TFD and applying \( | I \rangle \) from right to both sides of the given master equation, we can rewrite it in the following way
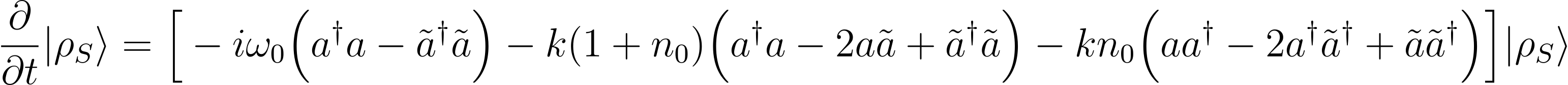
By taking: $$ K_{+} = a^\dagger \tilde{a}^\dagger, \hspace{3pt} K_{-} = a\tilde{a} $$ $$ K_{3} = \frac{1}{2}(a^\dagger a + \tilde{a}^\dagger \tilde{a} + 1)$$ $$K_{0} = (a^\dagger a – \tilde{a}^\dagger \tilde{a})$$ It can further be expressed as a Schrödinger like equation as
\begin{equation}
\frac{\partial }{\partial t}|\rho_S\rangle= -i\hat{H} |\rho_S\rangle
\end{equation}
Where \(-i\hat{H} = -i \omega_0 K_{0} + 2kn_0 K_{+} + 2k(1+n_0)K_{-} -2k(2n_0 + 1)K_3 + k \)
Since the above equation is in the form of a Schrödinger equation, its solution can easily be written to yield the following form:
\begin{equation}
|\rho_S (t)\rangle= \exp{\Big(\gamma_0 K_0 + kt\Big)}\exp{\Big(\gamma_{+} K_{+} + \gamma_3 K_3 + \gamma_{-} K_{-} \Big)} |\rho_S (0)\rangle \nonumber
\end{equation}
Where $$ \gamma_0 = -i\omega_0 t,\hspace{5pt}\gamma_{-} =2k(1+n_0)t $$ $$\gamma_3 = -2k(2n_0 + 1)t,\hspace{2pt}\gamma_{+} = 2kn_0t$$ $$ \gamma = 2k$$
References:
[1] Shanta, P., Chaturvedi, S., Srinivasan, V., & Kapoor, A.K. (1996). Operator methods for master equations in quantum optics. International Journal of Modern Physics B: Condensed Matter Physics; Statistical Physics; Applied Physics, 10(13/14), 1573. https://doi.org/10.1142/S0217979296000672
https://www.worldscientific.com/doi/abs/10.1142/S0217979296000672


